알고리즘
Adaboost
Small Octopus
2016. 4. 26. 22:16
1. Exponential Loss
Exponential 함수를 이용하여 Loss를 정의한다.
나중에 Loss를 최소화하는데 Exponential이 미분하기 좋기 때문이다.
함수는 x = -1일때 2.7 , x = 0 일때 1, x = 1 일때 0.37 이며
x가 커질 수록 작아진다. 예측결과와 GT가 같으면 적은 Loss을 틀리면 큰 Loss을 할당한다.
2. boosted classifier
아래와 같은 수식으로 표현된다.
어떤 샘플하나의 중요도가 처음 이었다면 중요도는 Loss 가 곱해지면서 아래와 같이 쓸 수 있다.
Exp Loss를 다시 쓰면
- Samples
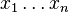
- Desired outputs

- Initial weights
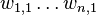 set to
set to 
- Error function
- Weak learners
![h\colon x \rightarrow [-1, 1]](https://upload.wikimedia.org/math/7/a/c/7ac84ec1f629adee8577e6e8097fede4.png)
For  in
in 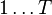 :
:
- Choose
- Find weak learner
 that minimizes
that minimizes  , the weighted sum error for misclassified points
, the weighted sum error for misclassified points 
- Choose
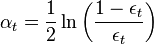
- ln(x)
- Add to ensemble:
- Update weights:
 for all i
for all i- Renormalize
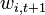 such that
such that 
- (Note: It can be shown that
 at every step, which can simplify the calculation of the new weights.)
at every step, which can simplify the calculation of the new weights.)
 :
: