The Beautiful Future
COMA 본문
Generating 3D faces using Convolutional Mesh Autoencoders ECCV 2018.
Abstract
기존 방법은 선형 서브 공간 또는 고차원 텐서 일반화를 사용했다. 이 선형성 때문에 극한 변형과 비선형 표정을 캡쳐할 수 없었다.
그리서 얼굴 비선형 표현할수 있는 모델을 제안하며 spectral convolutions을 mesh surface에 적용함으로써 가능하다.
계층적 mesh 표현이 가능한 mesh sampling operation을 사용해서 shape과 expression의 비선형 변형을 멀티스케일로 캡쳐한다.
variational setting으로 우리의 모델은 multivariate Gaussian distribution으로 다양한 리얼 3D faces을 뽑아낼수 있다.
학습 데이터셋은 12명의 20,466 mesh가 사용되었고 제한적인 데이터양에 비해서 75%의 적은양의 파라미터를 사용하면서 50% 적은 리컨스트럭션 에러를 보인다.
3. Mesh Operators
F = ( V, A), V ∈ R^nx3, A ∈ {0,1}^nxn
Aij =1 에지 커텍션 연결됨, Aij=0 에지 커넥션 연결안됨.
non-nromalized Laplacian: L = D - A, Dii = sum_j Aij
[15] Spectral graph theory. No. 92, American Mathematical Soc. (1997) <-- graph fourier transform
diagonalized Laplacian: L = U∧U^T,
fourier basis: U ∈ R^nxn, U=[u_1, u_2, ... , u_n-1]
eigen vector of L : u_i
∧ = diag([λ_1, ..., λ_n-1] ) ∈ R^nxn
mesh vertices : x ∈ R^nx3
graph fourier transform: x_w = U^T x
inverse graph fourier transform: x = U^T x
3.1 Fast spectral convolutions
컨볼루션은 퓨리에 스페이스에서 하다마다프로덕트로 정의된다. x ∗ y = U ((U T x) (U T y))
U 매트릭스가 스파스하지 않기때문에 연산량이 많다. recursive Chebyshev polynomial [17, 23]
을 이용해서 메쉬 필터링 커널 g 쎄타를 정의 할수 있다.
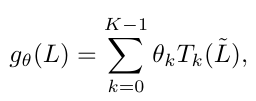
스케일드 라플라시안 L̃ = 2L/λmax − In ,
θ ∈ RK is a vector of Chebyshev coefficients.
Tk ∈ Rn×n is the Chebyshev polynomial of order k that can be computed recursively as Tk (x) = 2xTk−1 (x) − Tk−2(x)
T0 = 1 and T1 = x. The spectral convolution can then be defined as in [17]
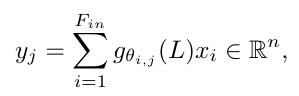
yj는 y ∈ Rn×Fout 의 j 번째 특징을 계산한다.
입력 x ∈ Rn×Fin 은 Fin 개의 특징을 가지고 있다.
face mesh 는 Fin = 3 개의 버텍스와 대응하는 포지션을 가지고 있다.
Each convolutional layer has Fin × Fout vectors of Chebyshev
coefficients, θi,j ∈ RK , as trainable parameters
3.2 Mesh Sampling
지역적 전역적 문맥을 캡쳐하기위해 hierarchical multi-scale representation를 사용한다.
지역적 문맥은 얕은 layer에서 캡쳐하고 전역적 문맥은 깊은 layer에서 캡쳐한다.
mesh를 nx3 tensor로 생각할 수 있다. 하지만 conv를 적용하면 디멘션이 달라진다.
mesh sampling operation을 적용하면 이웃 vertex 컨테스트를 유지한다.
quadric matrices [20] Surface simplification using quadric error metrics. Computer graphics and interactive
techniques 1997.
m개의 vertex를 가지는 mesh를 down-sampling 한다고 하면
down-sample transform metrices Qd ∈ {0,1}^nxm, up-sample transform matrices Qu ∈ R^mxn, m > n.
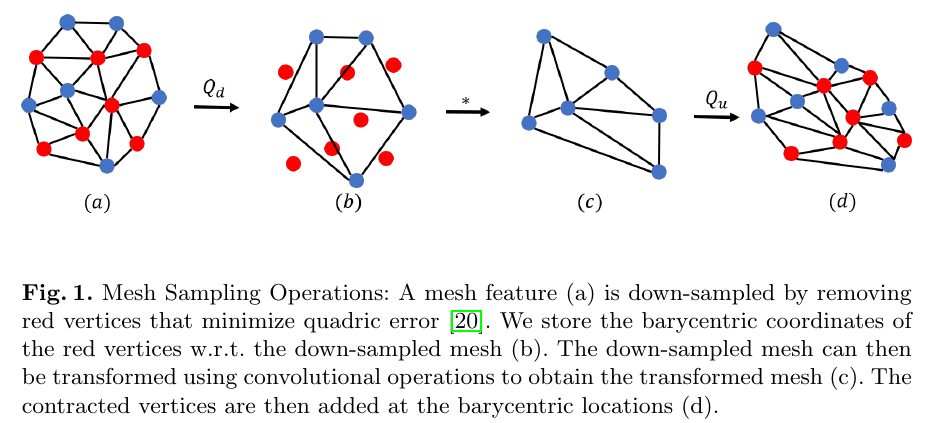
다운 샘플링은 정점 쌍을 반복적으로 축소하여 얻습니다. quadric matrices [20]를 이용하여 표면 오차 근사를 유지하도록 축소.
아래그림 (a) 에서 빨간점이 축소된다. 남은 파란 점들이 원본메쉬의 서브셋이다. Vd ⊂ V.
q: 원본 vertex, m개
p: down sample된 vertex, n개
Qd (p, q) ∈ {0, 1} 은 down-sampling되는 동안 q vertex를 살릴지 버릴지를 나타낸다.
무손실 다운샘플링 업샘플링은 일반곡면에 구현불가능하기때문에 다운샘플링하면서 업샘플링 매트릭스를 구축한다.
Vd에 convolution이 적용된다(b -> c). (c)에 남은 vertex들은 업샘플링하는동안 유지된다(c->d).
다운샘플링되었던 빨강 vertex들은 다운샘플된 메쉬 면에 barycentric coordinates를 이용해서 맵핑된다.
(b)에서 버려진 빨강 v는 가장 가까운 tri (i, j, k)로 프로젝션되어 부터 barycentric 가중치 wivi + wjvj + wkvk로 표현된다.
이 가중치는 Qu에 업데이트되어서 Qu (q, i) = wi , Qu (q, j) = wj , and Qu(q, k) = wk , and Qu (q, l) = 0 otherwise.
Vu = Qu Vd.
Chebyshev convolutional filters with K = 6 Chebyshev polynomials.
[21] biased ReLU[21], Deep sparse rectifier neural networks, Artificial Intelligence and Statistics (2011)
'논문' 카테고리의 다른 글
| Facial Expression Retargeting from Human toAvatar Made Easy (0) | 2023.01.26 |
|---|---|
| Attention Mesh: High-fidelity Face Mesh Prediction in Real-time (0) | 2022.12.28 |
| 3D Shape Regression for Real-time Facial Animation TOG2013 (0) | 2022.08.27 |
| Facial Retargeting with Automatic Range of Motion Alignment (0) | 2022.08.20 |
| Realtime Performance-Based Facial Animation (0) | 2022.08.14 |



